中学数学问题(十二道)
目录
初中数学问题
二次函数
【1】.
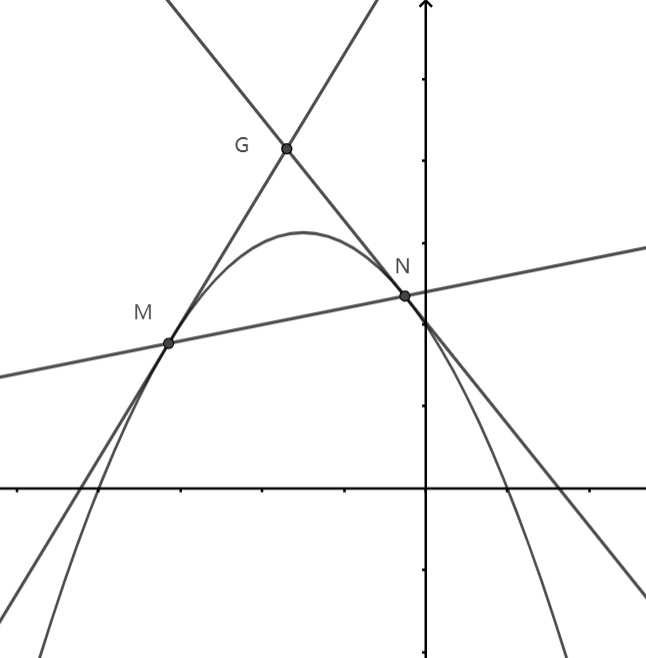
待定系数法设好过(-1,1)的直线的解析式为y=k(x+1)+1。那么联立直线与抛物线的解析式,可以用含k的式子表示出M,N的横纵坐标(实际上表示出来很复杂,有根式)。理论上,我们可以继续待定系数法,引入参数m,和k一起表示过M点的直线;引入参数n,和k一起表示过N点的直线。再根据与抛物线相切,即两直线分别与抛物线方程联立,消元得到的新方程的判别式应该等于0。由此得到的两个关系式,理论上可以得到m,n与k的关系,从而消掉m,n。即是说,我们理论上可以用k表示出分别过M,N的两条切线的方程,从而求出二者的交点G。事实上,以上分析从第一步就打止了,因为M,N的横坐标解出来是一个含有根式的复杂式子。
本题的正确解法是,待定直线的解析式为y=k(x+1)+1后,联立直线与抛物线的解析式,利用韦达定理,得到两根之和与两根之积的表达式。然后MG,NG两条直线分别也和抛物线方程联立,利用韦达定理,从而用两个根(即M,N的横坐标)表示出两条直线的解析式。最后利用一开始得到的两根之和与两根之积的表达式,消去k,求G点的坐标,得到其横纵坐标的一个关系式。
高中数学问题
集合与逻辑用语
【2】.某班45名学生参加植树节活动,每位学生都参加除草、植树活动。依据表现,被评定为优秀,合格两个等级,结果如下表。若在两个项目中都合格的学生最多有10人,则在两个项目中都优秀的人数最多是多少?
| 劳动项目 | 优秀 | 合格 | 合计 |
|---|---|---|---|
| 除草 | 30 | 15 | 45 |
| 植树 | 20 | 25 | 45 |
都合格的最多10人,那么假设都合格的是10人,从植树这一项目来看,则会有植树合格的15人,他们的除草是优秀.即一优一合格的会有至少15人,那么都优的最多只能有20人.
【3】.角A,B是 三角形 ABC 的两个内角,下列四个条件下,A>B 的充要条件是

此题角A,B是三角形的内角,这有一个容易忽视的隐含条件,即A+B<180,也就是说A+B的一半小于90.这是一个比较强的条件,最后分析此条件下三角函数的变化,最后发现答案是A.如果没有注意到这个条件,此题就分析不出来.
不等式
【4】.
 |
 |
这里思考了很久,因此记录思考一下。这种解法有问题。图中画下划线部分,m,n的平方和大于等于2mn,但是2mn并不是m,n平方和的最小值。左边的式子与右边的式子,可以看作同一个三维坐标系下两个曲面必然具有的一种关系。但是m,n的平方和的最小值是0,在这个题目的具体限制条件下则另有答案。无论如何,关于某些变量的式子 与 另一个式子的大小比较,不意味着前式的最值。求其最值应该是求出一个确定的值才对,而不是另一个函数。